W części I podane zostały niezbędne wiadomości dotyczące projektowania i wykonywania ogrodzeń z klinkieru. Do omówienia pozostaje jeszcze bardzo istotna przy budowie ogrodzeń część konstrukcyjna.

Zagadnienia konstrukcyjne przy budowie ogrodzeń odnoszą się przede wszystkim do słupków przybramowych, które muszą mieć odpowiednią wytrzymałość oraz do ich fundamentów, stanowiących o stateczności ogrodzenia.

Jak zatem przystąpić do projektu wspomnianych już słupków przybramowych? Przede wszystkim należy ustalić (przyjąć) parametry geometryczne ogrodzenia, czyli:

a) głębokość posadowienia: 0,8 do 1,2 m zależnie od strefy klimatycznej,
b) nośność podłoża gruntowego (określa ją projektant na podstawie badań podłoża w wykopie próbnym w pobliżu ogrodzenia),
c) projektowane wymiary geometryczne ogrodzenia:

• przekrój poprzeczny słupków (najczęściej przyjmuje się 38 x 38 cm),
• wysokość cokołu,
• wysokość słupków nad cokołem,
• rodzaje przęseł (drewno, metal),
• szerokość bramy wjazdowej. Szerokość bramy w świetle wg przepisów prawa budowlanego powinna wynosić nie mniej niż 2,4 m. W praktyce przyjmuje się z reguły 3,0 m lub więcej,
• szerokość furtki wg przepisów, co najmniej 0,9 m; w praktyce jest to z reguły 1,0 m lub nieco więcej,
• sposób otwierania furtki (czy zawiasy furtki są na tym samym słupku, co skrzydło bramy).

Mając te dane ustala się obciążenia wynikające z geometrii i konstrukcji ogrodzenia (ciężar własny) oraz obciążenia technologiczne i montażowe wg norm budowlanych.

Ciężar własny

• dla konstrukcji klinkierowych: γ = 19,0 kN/m³,
• dla żelbetu: γ = 24,0 kN/m³,
• dla betonu: γ = 23,0 kN/m³,
• dla przęseł i skrzydeł metalowych: γ = 0,50 kN/m³ lub wg rzeczywistego ciężaru,
• dla przęseł i skrzydeł drewnianych ażurowych: γ = 0,10 kN/m³,
• dla przęseł i skrzydeł drewnianych pełnych: γ = 0,20 kN/m³,
• ciężar gruntu (na odsadzkach fundamentu): γ = 20,0 kN/m³

Pozostałe obciążenia

• siła skupiona na końcu skrzydła bramy P = 1,0 kN. Jest to najmniejsza wartość obciążenia pionowego skupionego, jaką powinien przenieść każdy element konstrukcyjny, na którym może stanąć noga człowieka z narzędziami (wg PN-82/B-02003),
• obciążenie poziome 0,3 kN/m w ogrodzeniach miejsc przeznaczonych do przebywania pojedynczych ludzi,
• obciążenie poziome wyjątkowe od uderzenia pojazdem wg normy PN-82/B-02004 dla samochodów osobowych i furgonetek H = 20 kN na wysokości h = 1,0 m od poziomu jezdni. Jest to obciążenie wyjątkowe γ_f = 1,0.

Obciążenie śniegiem wg PN-80/B-02010 nie ma wpływu na wymiarowanie konstrukcji. Natomiast obciążenie wiatrem wg PN-77/B-02011 musi być uwzględnione przy projektowaniu ogrodzenia.

Jednoczesność działania obciążeń

a) Ciężar własny działa zawsze.
b) Siła skupiona na końcu skrzydła bramy bez obciążenia wyjątkowego uderzeniem pojazdu.
c) Siła pozioma uderzenia pojazdem bez obciążenia siłą skupioną na końcu skrzydła.
Zatem obciążenia mogą działać w zestawie: a + b lub a + c. Zestaw a + c obciąża słupki bardziej.

Przykład

Rys. 1 Geometria ogrodzenia

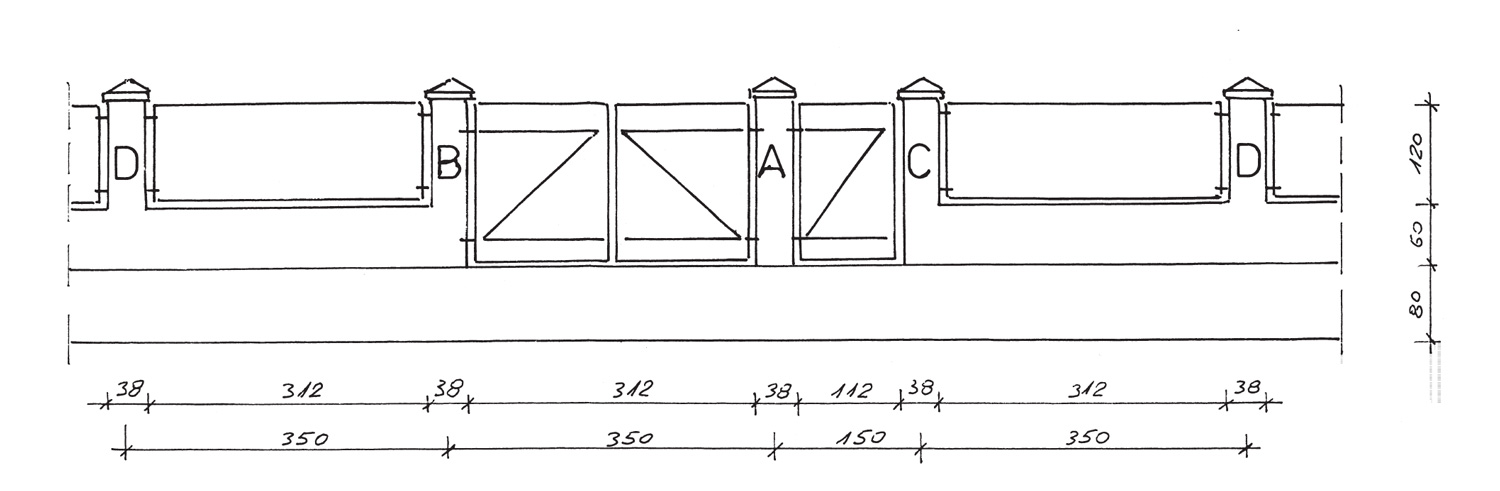
Ogrodzenie o wymiarach jak na rysunku obok.

1. Wysokość ogrodzenia h = 1,80 m nad terenem, w tym cokół o wysokości 0,60 m,
2. rozstaw osiowy słupków – co 3,50 m,
3. przęsła, skrzydła bramy i skrzydło furtki metalowe o ciężarze = 0,50 kN/m²,
4. słupki pośrednie o przekroju 38 x 25 cm,
5. słupki przybramowe o przekroju 38 x 38 cm,
6. grubość cokołu 25 cm,
7. głębokość posadowienia h_p = 0,80 m,
8. dopuszczalne naciski na podłoże gruntowe δ = 1,5 daN/cm²
9. zawiasy furtki na tym samym słupku co zawiasy skrzydła bramy,
10. rozstaw osiowy słupków przybramowych I₁ = 3,50 m.

Stąd światło bramy I₁ = 3,50 – 0,38 = 3,12 m

1. rozstaw słupków przy furtce I₂ = 1,50 m

Stąd światło furtki I₂ = 1,50 – 0,38 = 1,12 m

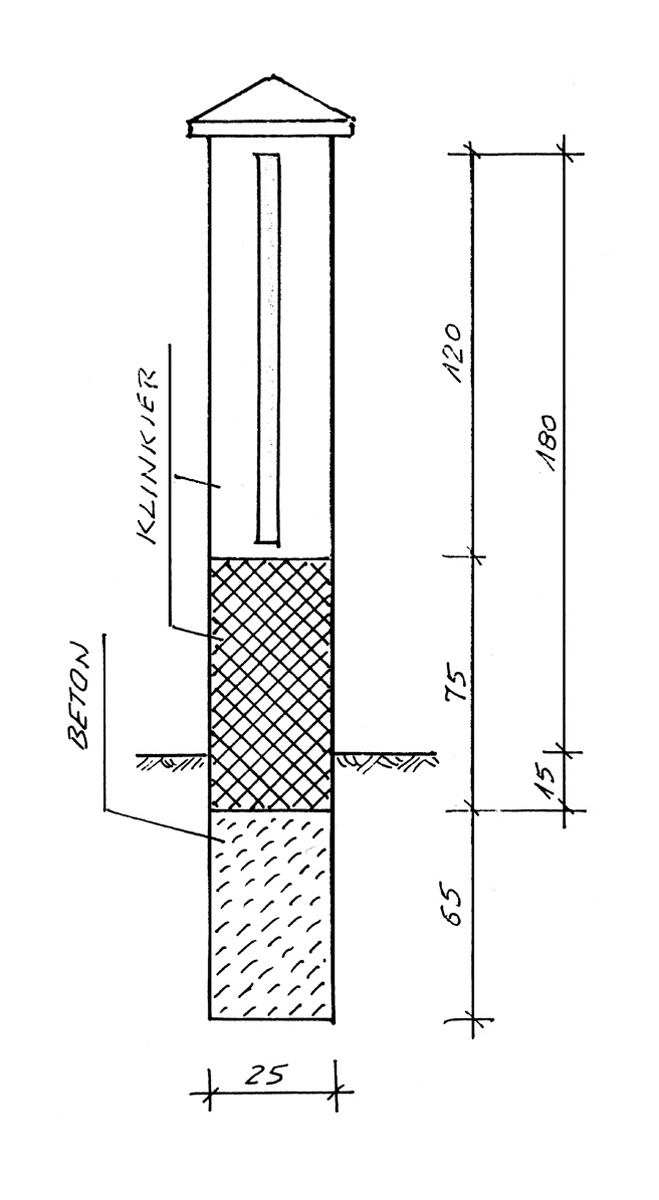
1. cokół i słupki z klinkieru; rdzeń słupków żelbetowy,
2. poniżej klinkieru fundament betonowy.

Obliczenia poniżej są podane dla tego właśnie przykładu.

Rodzaje słupków pod względem obciążenia i konstrukcji

Słupek A: 38 x 38 cm, obciążenie skrzydłem bramy i furtki, narażony na uderzenie pojazdem,
Słupek B: 38 x 38 cm, obciążenie przęsłem ogrodzenia i skrzydłem bramy, narażony na uderzenie pojazdem,
Słupek C: 38 x 25 cm, obciążony przęsłem ogrodzenia z jednej strony,
Słupek D: 38 x 25 cm, obciążony przęsłami ogrodzenia z obydwu stron są to wszystkie słupki pośrednie w ogrodzeniu.

Najbardziej obciążony jest słupek A. Można go posadowić na różne sposoby. Może mieć tylko własną stopę fundamentową lub stopę w formie poszerzenia fundamentu ciągłego pod ogrodzenie o szerokości 25 cm. Najpierw policzymy posadowienie na własnej stopie fundamentowej.

Obciążenie:

• słupek z klinkieru (0,38 x 0,38 – 0,14 x 0,14) x 1,95 x 19,0 x 1,1 = 5,09 kN,
• rdzeń żelbetowy 0,14 x 0,14 x 1,95 x 24,0 x 1,1 = 1,01 kN,
• fundament 0,38 x 0,38 x 0,65 x 24,0 x 1,1 = 2,48 kN
• skrzydło bramy 1,56 x 1,80 x 0,50 x 1,2 = 1,68 kN
• skrzydło furtki 1,12 x 1,80 x 0,50 x 1,2 = 1,21 kN

Razem: 11,47 kN

Obciążenie poziome

Uderzenie pojazdem: H = 20,0 kN h₁ dla słupka = 1,15 m h₂ dla fundamentu = 1,80 m.
Kierunek działania obciążenia prostopadły do linii ogrodzenia.
Do momentów zginających od:

• bramy P₁ = 1,68 kN e₁ = 1,56 x 0,5 + 0,19 = 0,97 m
• furtki P₂ = 1,21 kN e₂ = 1,12 x 0,5 + 0,19 = 0,75 m

Kierunek działania równoległy do linii ogrodzenia i prostopadły do niej.
Siła skupiona P₃ = 1,0 x 1,2 = 1,2 kN:
= dla bramy e₃ = 1,56 + 0,19 = 1,75 m
= dla furtki e₃ = 1,12 + 0,19 = 1,31 m
Jednoczesność działania sił: H + P1 + P2 lub: P1 + P2 + P3

Sprawdzenie wytrzymałości słupków w poziomie nad fundamentem

Obciążenie pionowe N = 11,47 – 2,48 = 8,99 kN
Obciążenie poziome H = 20,00 kN

Rys. 2a. Konstrukcja Słupków przybramowych odpornych na urzedzenie pojazdem

Momenty zginające:

1. równolegle do linii ogrodzenia: M = P₁ x e₁ – P₂ x e₂ + P₃ x e₃ = 1,68 x 0,97 – 1,21 x 0,75 + 1,20 x 1,75 = 2,82 kNm
2. prostopadle do linii ogrodzenia: M = 1,68 x 0,97 + 1,21 x 0,75 + 20,00 x 1,15 = 25,54 kNm

F = 38 x 38 = 1444 cm²

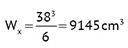
Naprężenia w kierunku równoległym do linii ogrodzenia:

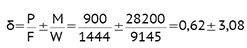
δ₁ = 0,62 + 3,08 = 3,70 daN/cm²

δ₂ = 0,62 – 3,08 = -2,46 daN/cm²

Naprężenia w kierunku prostopadłym do linii ogrodzenia:

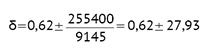
δ₁ = 0,62 + 27,93 = 28,55 daN/cm²

δ₂ = 0,62 – 27,93 = -27,31 daN/cm²

Przy klinkierze kl. 25 MPa i zaprawie marki R_z = 5 MPa
R_mk = 3,6 MPa dla ściskania ϒ_m = 1,5

Ze względu na przekrój F = 0,1444 m² < 0,30 m²
ϒ_m1 = 1,38

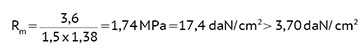
bez uwzględnienia
uderzenia pojazdem

Dla ścinania R_t = 0,3 MPa
δ_t = 2000 : 1444 = 1,39 daN/cm² < 3,0 daN/cm²

Dla rozciągania przy zginaniu
ϒ_m = 1,7 i ϒ_m1 = 1,38

2,46 daN/cm² < 27,31 daN/cm²
przy uderzeniu pojazdem.
Rdzeń słupka musi być zbrojony.

Przypadek bez uderzenia pojazdem

M = 1,68 x 0,97 + 1,21 x 0,75 + 1,2 X 1,75 + 1,2 x 1,31 = 6,21 kNm

Beton B 15 R_b = 8,7 Mpa stal A – III 34GS R_a= 350 Mpa
b = 14 cm, h₀ = 14 – 2 = 12 cm

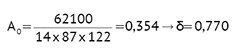
Przyjmuję 2 Ø 12 o F_a = 2,28 cm²

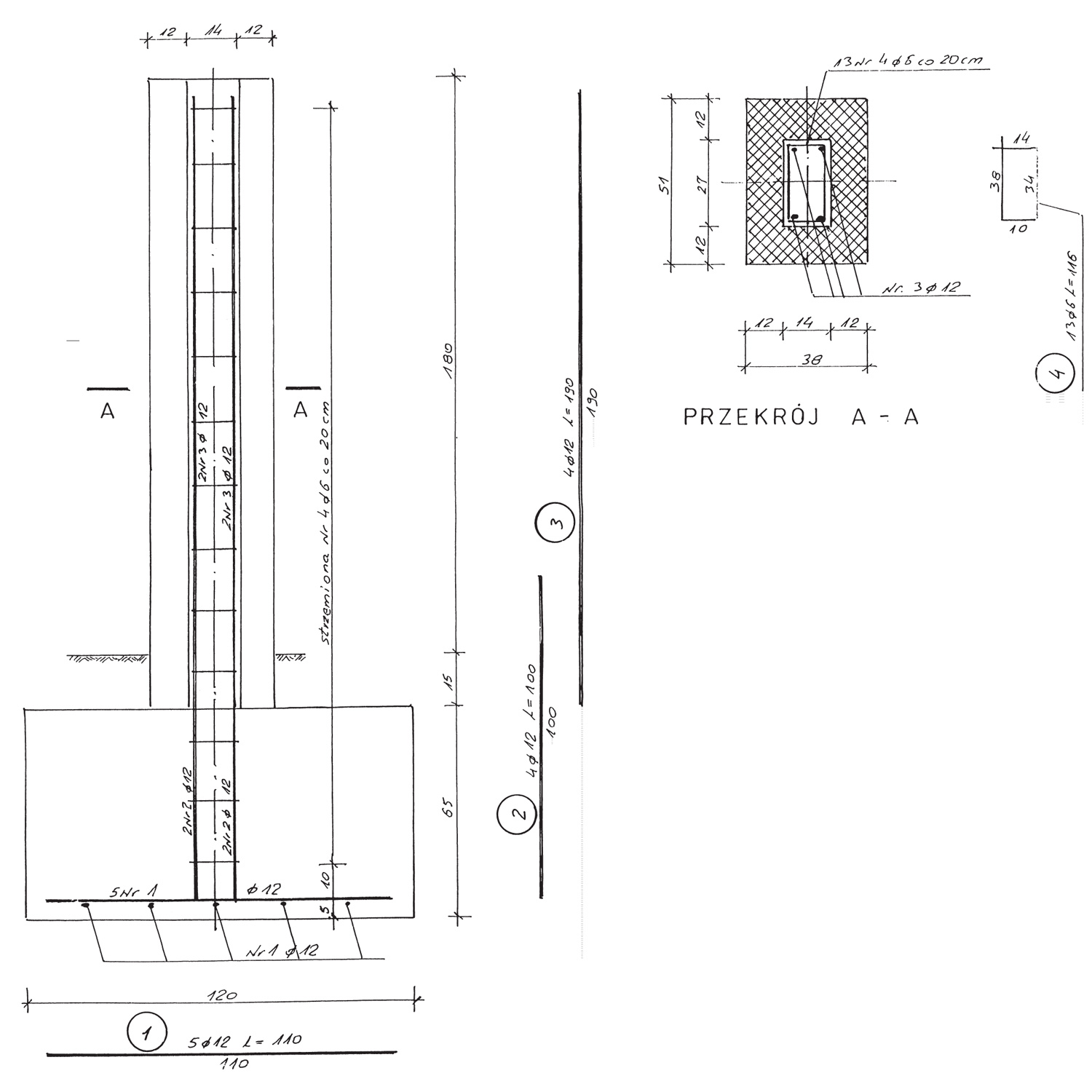
Aby zabezpieczyć słupek przed skutkiem uderzenia pojazdem, trzeba zwiększyć przekrój słupka do wymiarów 38 x 51 cm czyli 1,5 x 2 cegły. Wówczas rdzeń żelbetowy będzie miał przekrój 14 x 27 cm.

Rys. 2b. Konstrukcja słupków przybramowych nieodpornych na urzedzenie pojazdem

Ciężar słupka

Dla klinkieru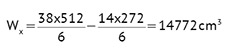

ΔM = 14772 x 1,7 = 25112 daNcm = 2,51 kNm
Dla rdzenia M = 25,54 – 2,51 = 23,03 kNm
b = 14 cm h₀ = 27 – 2 = 25 cm

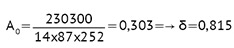
Fundament pod słup

Przyjmuję stopę fundamentową o wymiarach 120 x 120 cm.

Obciążenie pionowe

Fundament 1,2 x 1,2 x 0,65 x 24,0 x 1,1 = 24,71 kN

Razem obciążenie pionowe:
N = 11,20 kN + 29,20 kN = 40,40 kN
F = 120 x 120 = 14400 cm²

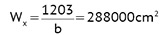
M = 20,00 x 1,80 + 1,68 x 0,97 + 1,21 x 0,75 = 38,54 kNm

Nacisk na podłoże gruntowe

δ1 = 0,28 + 1,34 = 1,62 daN/cm²
δ2 = 0,28 – 1,34 = -1,06 daN/cm²

Słupek B ma tylko nieco mniejsze obciążenie ze względu na brak obciążenia furtką. Konstrukcja słupka i jego posadowienie są takie same jak słupka A.
Słupek C jest najmniej obciążony, bo tylko połową przęsła.
Słupki D są to wszystkie pośrednie słupki ogrodzenia.

Fundament pod cokół i słupki D, betonowy, o wymiarach szerokość 25 cm i wysokość 65 cm.

Obciążenie

Ciężar własny na 1 mb ogrodzenia q = 32,74 : 3,50 = 9,35 kN/m

Obciążenie poziome wiatrem według PN-77/B-02011 dla I strefy

P = q_k x c x c_e x β x ϒ_f
gdzie:
q_k = 0,25 kN/m²
c_e = 0,7 dla terenu „C”, ponieważ ogrodzenie jest budowlą niską w stosunku do wysokości budynku i drzew,
c = 0,96 wg Z1-19 przy założeniu 70% prześwitu

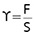
(F = suma powierzchni rzutów wszystkich elementów ogrodzenia na jego płaszczyznę , S = h x l = powierzchnia ogrodzenia)

Przy γ = 0,30 C = 0,96
β = 1,8
γ_f = 1,3
ρ = 0,25 x 0,7 x 0,96 x 1,8 x 1,3 = 0,39 kN/m²
Dla 1 = 3,50 m i h = 1,80 m mamy F = 3,50 x 1,80 = 6,30 m
P = 0,39 x 6,30 = 2,46 kN h = 0,90 m od terenu
Dla słupka h = 0,90 – 0,60 = 0,30 m
M = 2,46 x 0,30 = 0,74 kNm
F = 25 x 38 = 950 cm²

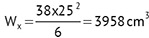
Ciężar słupka z przęsłem N = 2,38 + 2,25 = 4,63 kN

δ₁ = 0,49 + 1,87 = 2,36 daN/cm² < 17,4 daN/cm²
δ₂ = 0,49 – 1,87 – -1,38 daN/cm² < 1,7 daN/cm²

Fundament

Obciążenie: q = 9,35 kN/m

Od parcia wiatru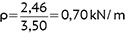

h = 0,90 + 0,80 = 1,70 m

M = 0,70 x 1,70 = 1,19 kNm

F = 25 x 100 = 2800 cm²

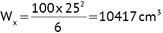
Naprężenia na grunt:

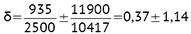
δ₁ = 0,37 + 1,14 = 1,51 daN/cm²
δ₂= 0,37 – 1,14 = – 0,77 daN/cm²

Rozpatrzmy jeszcze, jaki powinien być fundament pod słupek przybramowy w przypadku nie uwzględnienia uderzenia pojazdem.

– słupek ma przekrój 38 x 38 cm,
– rdzeń żelbetowy 14 x 14 cm ze zbrojeniem 2 O 12,
– obciążenie pionowe q = 11,47 kN + fundament i ziemia na odsadzkach,
– moment zginający M = 6,21 kNm.
Przyjmuję fundament o wymiarach w rzucie 70 x 70 cm

Ciężar fundamentu:

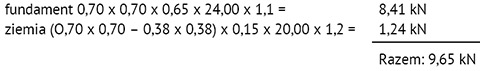
Razem N = 9,65 + 11,47 = 21,12 kN
F = 70 x 70 = 4900 cm²

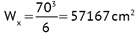
Naciski na podłoże gruntowe:

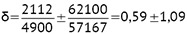
δ₁ = 0,59 + 1,09 = 1,68 daN/cm²
δ₂ = 0,59 – 1,09 = -0,50 daN/cm²

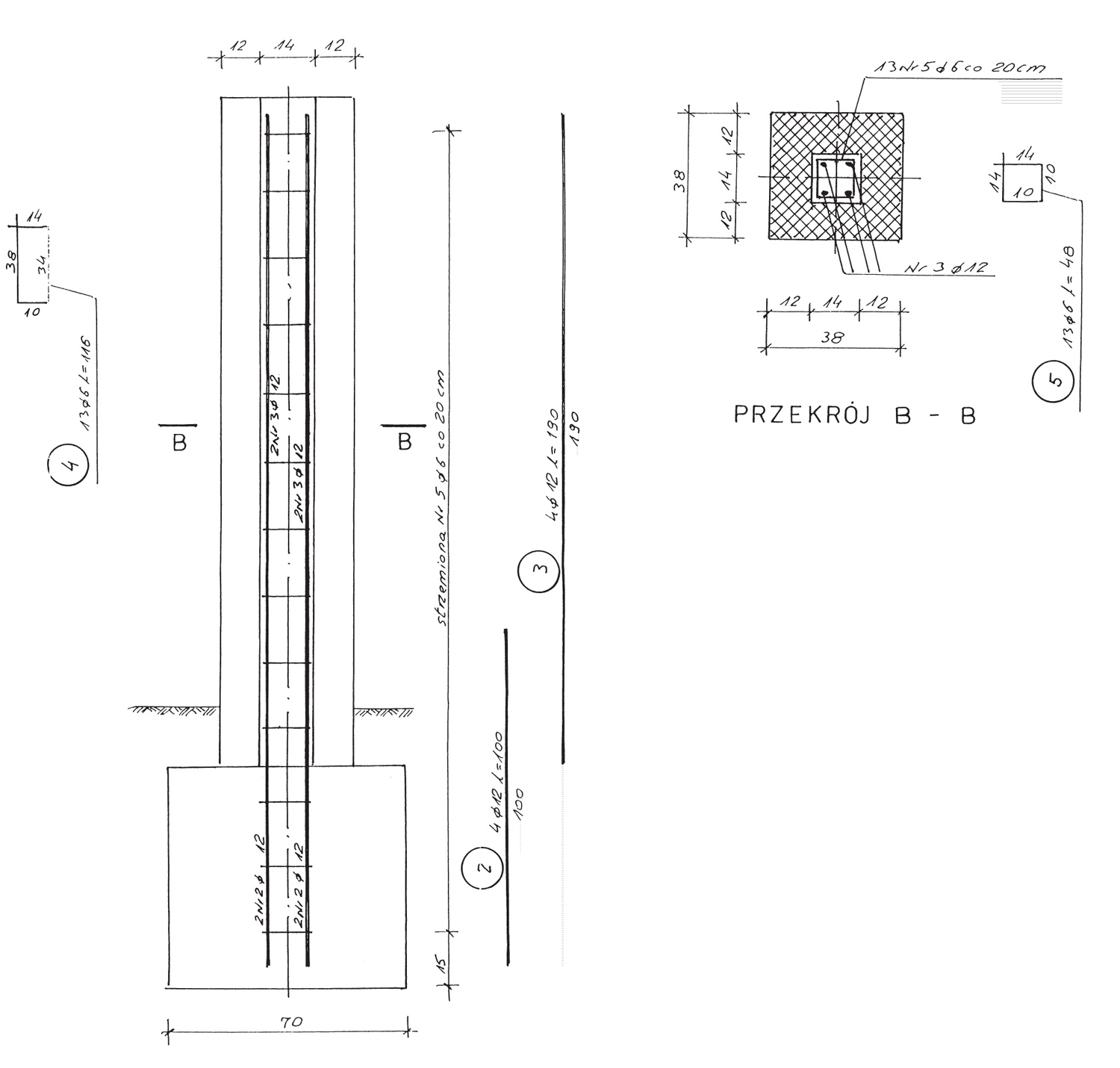
Okazuje się, że różnica w masie betonowej fundamentów pod słupki przybramowe w obydwu przypadkach jest niewielka. Przy uwzględnieniu uderzenia pojazdem fundament ma wymiary 120 x 120 cm – masa betonu V = 0,936 m³, natomiast przy pominięciu uderzenia pojazdem wymiary stopy wynoszą 70 x 70 cm, a masa betonu wynosi V₁ = 0,319 m³. Różnica wynosi: V – V1 = 0,517 m³. Dla dwóch słupków będzie to około 1 m³ betonu. Oszczędność niewielka, a strata może być duża w przypadku uderzenia pojazdem, a to zawsze jest możliwe. Na rys. 2 przedstawiona jest konstrukcja słupków przybramowych w dwóch wariantach:

a) przy uwzględnieniu uderzenia pojazdem i
b) z pominięciem uderzenia pojazdem

Na zewnątrz oba warianty prawie się nie różnią, ponieważ większy wymiar przekroju słupka wysunięty jest w kierunku posesji, a ten widok przesłania skrzydło bramy i przęsła ogrodzenia. Tak przedstawiony rysunek konstrukcji słupków przybramowych w projekcie ogrodzenia nie budzi żadnych wątpliwości wykonawcy robót budowlanych przy realizacji zadania. Na opisanym wyżej przykładzie widać więc, jak ważny jest projekt techniczny przy wykonywaniu robót budowlano-montażowych.

Wnioski końcowe

Z powyższego przykładu widać, że przy ogrodzeniu ażurowym fundament szerokości 25 cm, równy szerokości cokołu, jest odpowiedni przy dopuszczalnych naciskach na podłoże gruntowe rzędu 1,5 daN/cm². Przy ogrodzeniach pełnych z lekkimi przęsłami z drewna, fundament pod cokół (ogrodzenie) musi być odpowiednio szerszy. Jeśli chodzi o słupki przybramowe, to wymagają one obliczeń statycznych i wymiarowania. W przypadku nie uwzględniania uderzenia pojazdem, słupki przybramowe i ich fundamenty mogą być mniejsze, ale w praktyce to się nie opłaca. Zawsze jest możliwość uderzenia pojazdem przy wjeździe na posesję. W przypadku nie uwzględnienia tego w projekcie, po uderzeniu pojazdem słupek ulegnie złamaniu, a fundament odkształceniu i przesunięciu. Zachodzi wtedy potrzeba rozebrania uszkodzonej konstrukcji i wykonania jej od nowa. W wariancie uwzględniającym uderzenie najwyżej zostanie uszkodzonych kilka cegieł klinkierowych, łatwych do wymiany.

Jeszcze wniosek ogólny. Każde ogrodzenie jest inne, ma inne wymiary geometryczne i inną konstrukcję. W każdym przypadku projektantkonstruktor musi opracować część konstrukcyjne w formie obliczeń statycznych i odpowiednich rysunków.

Inwestorzy powinni o tym pamiętać. Dobrze opracowany projekt i zgodne z nim wykonawstwo gwarantuje stateczność i trwałość ogrodzenia. Klinkier jest materiałem budowlanym stosunkowo drogim, ale o wysokich parametrach użytkowych (wytrzymałość i estetyka).

Edmund Ratajczakk
Rysunki: Autor
Świat Klinkieru i Dachówek